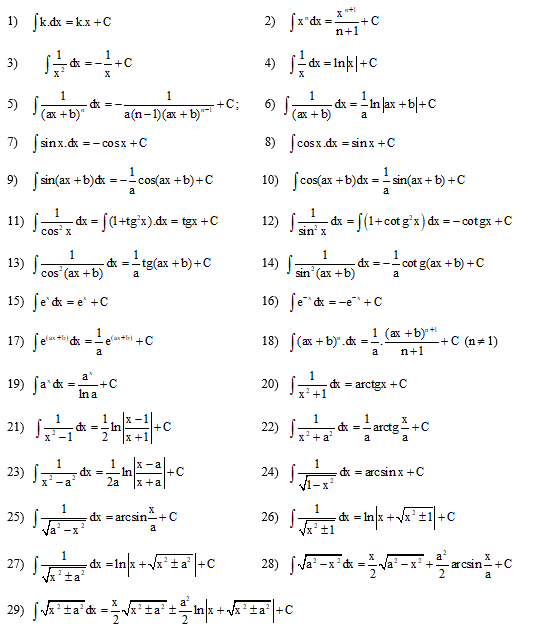1. Nguyên hàm
a) Khái niệm
Nếu \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\) trên \(K\) thì họ nguyên hàm của \(f\left( x \right)\) trên \(K\) là: \(\int {f(x)} dx = F(x) + C,C \in R.\)
b) Tính chất
+)\(\int {f'(x)} dx = f(x) + C\)
+)\(\int {\left[ {f(x) \pm g(x)} \right]} dx = \int {f(x)} dx \pm \int {g(x)} dx\)
+)\(\int {kf(x)} dx = k\int {f(x)} dx , (k \ne 0)\)
c) Nguyên hàm của một số hàm số thường gặp
d) Các phương pháp tìm nguyên hàm
- Sử dụng bảng nguyên hàm cơ bản
- Sử dụng phương pháp đổi biến số và từng phần để tìm nguyên hàm.
2. Tích phân
a) Định nghĩa
Cho hàm số \(f\left( x \right)\) liên tục trên khoảng \(I\) và \(a,b\) là hai số bất kì thuộc \(I.\) Nếu \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\) thì hiệu số \(F\left( b \right) - F\left( a \right)\) được gọi là tích phân của \(f\left( x \right)\) từ \(a\) đến \(b\) và kí hiệu là \(\int\limits_a^b {f(x)dx}.\)
Ta có công thức Newton – Leibnitz:
\(\int\limits_a^b {f(x)dx} = \left. {F\left( x \right)} \right|_a^b = F\left( b \right) - F\left( a \right)\)
b) Tính chất
+) \(\int\limits_a^a {f(x)dx} = 0\)
+) \(\int\limits_a^b {f(x)dx} = - \int\limits_b^a {f(x)dx} \)
+) \(\int\limits_a^c {f(x)dx} = \int\limits_a^b {f(x)dx} + \int\limits_b^c {f(x)dx} \)
+) \(\int\limits_a^b {kf(x)dx} = k\int\limits_a^b {f(x)dx} ,k \in R\)
+)\(\int\limits_a^b {[f(x) \pm g(x)]dx} = \int\limits_a^b {f(x)dx} \pm \int\limits_a^b {g(x)dx} \)
c) Phương pháp tính tích phân
Sử dụng công thức Newton – Leibnitz kết hợp với bảng nguyên hàm cơ bản ở trên và các phương pháp đổi biến số, từng phần để tính tích phân.
Ngoài ra còn có phương pháp sử dụng máy tính Casio sẽ được giới thiệu ở phần sau.
3. Ứng dụng của tích phân
a) Tính diện tích hình phẳng
+) Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\) (\(f\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\)), trục \(Ox\) và hai đường thẳng \(x = a\) và \(x = b\) được cho bởi công thức: \(S = \int\limits_a^b {\left| {f(x)} \right|dx} \)
+) Diện tích hình phẳng giới hạn bởi hai đường thẳng \(x = a,x = b\) và đồ thị của hai hàm số \(y = {f_1}\left( x \right)\) và \(y = {f_2}\left( x \right)\) (\({f_1}\left( x \right)\) và \({f_2}\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\)) được cho bởi công thức \(S = \int\limits_a^b {\left| {{f_1}(x) - {f_2}(x)} \right|dx} \)
b) Diện tích hình tròn và hình elip
+) Hình tròn bán kính \(R\) có diện tích \(S = \pi {R^2}\)
+) Hình elíp \(\left( E \right):\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\) có diện tích \(S = \pi ab\)
c) Tính thể tích vật thể, khối tròn xoay
+) Thể tích vật thể \(T\) có thiết diện \(S\left( x \right)\) được cho bởi công thức: \(V = \int\limits_a^b {S(x)dx} \)
+) Cho hàm số \(y = f\left( x \right)\) liên tục và không âm trên đoạn \(\left[ {a;b} \right].\) Thể tích của vật thể tròn xoay sinh bởi miền \(\left( D \right)\) giới hạn bởi \(y = f\left( x \right),\;x = a,x = b,y = 0\) quay quanh trục \(Ox\) được cho bởi công thức: \(V = \pi \int\limits_a^b {{y^2}dx} = \pi \int\limits_a^b {{f^2}(x)dx} \)
+) Cho hàm số \(x = f\left( y \right)\) liên tục và không âm trên đoạn \(\left[ {a;b} \right].\) Tính thể tích vật thể tròn xoay sinh bởi miền \(\left( D \right)\) giới hạn bởi \(x = f\left( y \right),\;y = a,y = b,x = 0\) quay quanh trục \(Oy\) được cho bởi công thức: \(V = \pi \int\limits_a^b {{x^2}dy} = \pi \int\limits_a^b {{f^2}(y)dy} \)
d) Thể tích khối nón và khối chóp, khối nón cụt và khối cầu
+) Thể tích khối nón (khối chóp) có diện tích đáy bằng \(B\) và chiều cao \(h\) được cho bởi \(V = \dfrac{1}{3}Bh.\)
+) Thể tích khối nón cụt (khối chóp cụt) có diện tích hai đáy là B1, B2 và chiều cao h được cho bởi:
\(V = \dfrac{1}{3}\left( {{B_1} + {B_2} + \sqrt {{B_1}{B_2}} } \right)h\)
+) Thể tích của khối cầu có bán kính \(R\) được cho bởi: \(V = \dfrac{4}{3}\pi {R^3}\)