1. Sự đồng biến, nghịch biến của hàm số
Cho hàm số \(y = f\left( x \right)\), khi đó:
+) \(f'\left( x \right) > 0\) trên khoảng nào thì hàm số đồng biến trên khoảng đó.
+) \(f'\left( x \right) < 0\) trên khoảng nào thì hàm số nghịch biến trên khoảng đó.
Điều kiện để hàm số đồng biến, nghịch biến trên khoảng \(\left( {a;b} \right)\)
+) Để hàm số đồng biến trên khoảng \(\left( {a,b} \right)\) thì \(f'\left( x \right) \ge 0,\forall x \in \left( {a,b} \right)\).
+) Để hàm số nghịch biến trên khoảng \(\left( {a,b} \right)\) thì \(f'\left( x \right) \le 0,\forall x \in \left( {a,b} \right).\)
2. Cực trị của hàm số
Dấu hiệu 1:
+) Nếu \(f'\left( {{x_0}} \right) = 0\) hoặc \(f'\left( x \right)\) không xác định tại \({x_0}\) và nó đổi dấu từ dương sang âm khi qua \({x_0}\) thì \({x_0}\) là điểm cực đại của hàm số.
+) Nếu \(f'\left( {{x_0}} \right) = 0\) hoặc \(f'\left( x \right)\) không xác định tại \({x_0}\) và nó đổi dấu từ âm sang dương khi qua \({x_0}\) thì \({x_0}\) là điểm cực tiểu của hàm số.
*) Quy tắc 1: (dựa vào dấu hiệu 1)
+) Tính \(y'\)
+) Tìm các điểm tới hạn của hàm số. (tại đó \(y' = 0\) hoặc \(y'\) không xác định)
+) Lập bảng xét dấu \(y'\) và dựa vào bảng xét dấu và kết luận.
Dấu hiệu 2:
Cho hàm số \(y = f\left( x \right)\) có đạo hàm đến cấp \(2\) tại \({x_0}\).
+) \({x_0}\) là điểm cực đại \( \Leftrightarrow \left\{ \begin{array}{l}f'\left( {{x_0}} \right) = 0\\f''\left( {{x_0}} \right) < 0\end{array} \right.\)
+) \({x_0}\) là điểm cực tiểu \( \Leftrightarrow \left\{ \begin{array}{l}f'\left( {{x_0}} \right) = 0\\f''\left( {{x_0}} \right) > 0\end{array} \right.\)
*) Quy tắc 2: (dựa vào dấu hiệu 2)
+) Tính \(f'\left( x \right),f''\left( x \right)\).
+) Giải phương trình \(f'\left( x \right) = 0\) tìm nghiệm.
+) Thay nghiệm vừa tìm vào \(f''\left( x \right)\) và kiểm tra, từ đó suy kết luận.
3. Giá trị lớn nhất và giá tị nhỏ nhất của hàm số
Quy tắc tìm GTLN – GTNN của hàm số:
*) Quy tắc chung: (Thường dùng cho \(D\) là một khoảng)
- Tính \(f'\left( x \right)\), giải phương trình \(f'\left( x \right) = 0\) tìm nghiệm trên \(D.\)
- Lập BBT cho hàm số trên \(D.\)
- Dựa vào BBT và định nghĩa từ đó suy ra GTLN, GTNN.
*) Quy tắc riêng: (Dùng cho \(\left[ {a;b} \right]\)) . Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên \(\left[ {a;b} \right]\)
- Tính \(f'\left( x \right)\), giải phương trình \(f'\left( x \right) = 0\) tìm nghiệm trên \(\left[ {a,b} \right]\).
- Giả sử phương trình có các nghiệm \({x_1},{x_2},... \in \left[ {a,b} \right]\).
- Tính các giá trị \(f\left( a \right),f\left( b \right),f\left( {{x_1}} \right),f\left( {{x_2}} \right),...\).
- So sánh chúng và kết luận.
4. Tiệm cận của đồ thị hàm số
+) Đường thẳng \(x = a\) là TCĐ của đồ thị hàm số \(y = f\left( x \right)\) nếu có một trong các điều kiện sau:
\(\mathop {\lim }\limits_{x \to {a^ + }} y = + \infty \) hoặc \(\mathop {\lim }\limits_{x \to {a^ + }} y = - \infty \) hoặc\(\mathop {\lim }\limits_{x \to {a^ - }} y = + \infty \) hoặc \(\mathop {\lim }\limits_{x \to {a^ - }} y = - \infty \)
+) Đường thẳng \(y = b\) là TCN của đồ thị hàm số \(y = f\left( x \right)\) nếu có một trong các điều kiện sau:
\(\mathop {\lim }\limits_{x \to + \infty } y = b\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } y = b\)
5. Bảng biến thiên và đồ thị hàm số
a) Các dạng đồ thị hàm số bậc ba \(y = a{x^3} + b{x^2} + cx + d\)
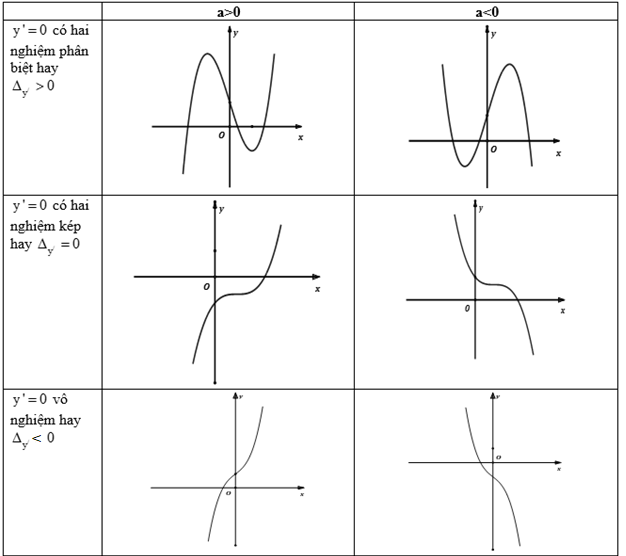
b) Các dạng đồ thị hàm số bậc bốn trùng phương \(y = a{x^4} + b{x^2} + c\)
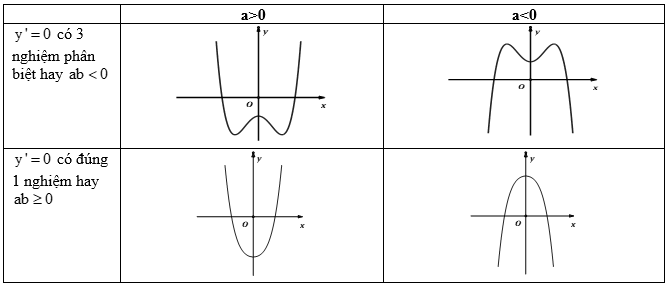
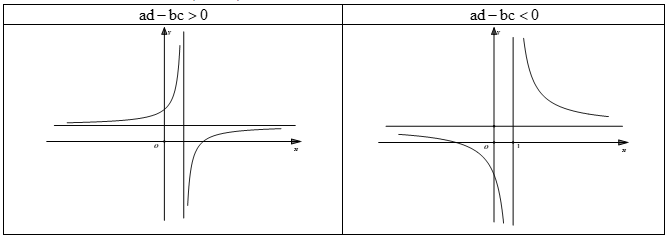
c) Các dạng đồ thị hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\)
+) Tập xác định: \(D = R\backslash \left\{ { - \dfrac{d}{c}} \right\}\)
+) Đạo hàm: \(y = \dfrac{{ad - bc}}{{{{\left( {cx + d} \right)}^2}}}\)
- Nếu \(ad - bc > 0\) hàm số đồng biến trên từng khoảng xác định. Đồ thị nằm góc phần tư \(2\) và \(4.\)
- Nếu \(ad - bc < 0\) hàm số nghịch biến trên từng khoảng xác định. Đồ thị nằm góc phần tư \(1\) và \(3.\)
+) Đồ thị hàm số có: TCĐ: \(x = - \dfrac{d}{c}\) và TCN: \(y = \dfrac{a}{c}\)
+) Đồ thị có tâm đối xứng: \(I\left( { - \dfrac{d}{c};\dfrac{a}{c}} \right)\)
6. Sự tương giao của đồ thị hàm số
a) Tìm giao điểm của hai đồ thị hàm số
Phương pháp:
Cho \(2\) hàm số \(y = f\left( x \right),y = g\left( x \right)\) có đồ thị lần lượt là \(\left( C \right)\) và \(\left( {C'} \right).\)
+) Lập phương trình hoành độ giao điểm của \(\left( C \right)\) và \(\left( {C'} \right):\)\(f\left( x \right) = g\left( x \right)\,\,\,\left( * \right)\)
+) Giải phương trình tìm \(x\) từ đó suy ra \(y\) và tọa độ giao điểm.
+) Số nghiệm của \(\left( * \right)\) là số giao điểm của \(\left( C \right)\) và \(\left( {C'} \right).\)
b) Tương giao của đồ thị hàm số bậc ba
Phương pháp 1: Bảng biến thiên (PP đồ thị)
+) Lập phương trình hoành độ giao điểm dạng \(F\left( {x,m} \right) = 0\) (phương trình ẩn \(x\) tham số \(m\))
+) Cô lập \(m\) đưa phương trình về dạng \(m = f\left( x \right)\)
+) Lập BBT cho hàm số \(y = f\left( x \right)\).
+) Dựa vào giả thiết và BBT từ đó suy ra \(m.\)
*) Dấu hiệu: Sử dụng PP bảng biến thiên khi \(m\) độc lập với \(x.\)
Phương pháp 2: Nhẩm nghiệm – tam thức bậc 2.
+) Lập phương trình hoành độ giao điểm \(F\left( {x,m} \right) = 0\)
+) Nhẩm nghiệm: (Khử tham số). Giả sử \(x = {x_0}\) là \(1\) nghiệm của phương trình.
+) Phân tích: \(F\left( {x,m} \right) = 0 \Leftrightarrow \left( {x - {x_0}} \right).g\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = {x_0}\\g\left( x \right) = 0\end{array} \right.\) (\(g\left( x \right) = 0\) là phương trình bậc \(2\) ẩn \(x\) tham số \(m\)).
+) Dựa vào yêu cầu bài toán đi xử lý phương trình bậc \(2\) \(g\left( x \right) = 0\).
