CHƯƠNG I. SỐ HỮU TỶ. SỐ THỰC
BÀI 1. TẬP HỢP Q CÁC SỐ HỮU TỈ
I. LÝ THUYẾT TRỌNG TÂM
1. Số hữu tỉ
+ Các phân số bằng nhau là cách viết khác nhau của cùng một số, số đó được gọi là số hữu tỉ.
+ Số hữu tỉ là số được viết dưới dạng phân số \[\frac{a}{b}\]với \[a,b\in \mathbb{Z}\]và \[b\ne 0\]
+ Tập hợp các số hữu tỉ được kí hiệu là \[\mathbb{Q}\] (\[x\] là số hữu tỉ thì ghi là \[x\in \mathbb{Q}\])
2. Biểu diễn các số hữu tỉ trên trục số
Để biểu diễn số hữu tỉ \[\frac{a}{b}\] (\[a,b\in \mathbb{Z}\];\[b>0\]) trên trục số ta làm như sau:
+ Chia đoạn đơn vị \[\left[ 0;1 \right]\]trên trục số thành \[b\] phần bằng nhau, mỗi phần là \[\frac{1}{b}\]được gọi là đơn vị mới .
+ Nếu \[a>0\]thì phân số \[\frac{a}{b}\]được biểu diễn bằng một điểm nằm bên phải điểm \[O\] và cách điểm \[O\] một đoạn bằng a lần đơn vị mới .
+ Nếu \[a<0\]thì phân số \[\frac{a}{b}\]được biểu diễn bằng một điểm nằm bên trái điểm \[O\] và cách điểm \[O\] một đoạn bằng \[\left| a \right|\] lần đơn vị mới .
3. So sánh hai số hữu tỉ
Để so sánh hai số hữu tỉ \[x,y\]ta thường làm như sau:
+ Viết \[x,y\]dưới dạng hai phân số có cùng mẫu dương
\[x=\frac{a}{m};y=\frac{b}{m}\left( a,b,m\in \mathbb{Z};m>0 \right)\]
+ So sánh hai số nguyên \[a\]và \[b\]
+ Nếu \[athì \[x
+ Nếu \[a=b\]thì \[x=y\]
+ Nếu \[a>b\]thì \[x>y\]
+ Trên trục số nếu \[xthì điểm \[x\] nằm bên trái điểm \[y\]
+ Số hữu tỉ lớn hơn \[0\] được gọi là số hữu tỉ dương.
+ Số hữu tỉ nhỏ hơn \[0\] được gọc là số hữu tỉ âm.
+ Số \[0\] không phải là số hữu tỉ dương cũng không phải là số hữu tỉ âm.
Nhận xét:
+ Số hữu tỉ \[\frac{a}{b}\]là số hữu tỉ dương (\[\frac{a}{b}>0\]) thì \[a,b\]cùng dấu.
+ Số hữu tỉ \[\frac{a}{b}\]là số hữu tỉ âm (\[\frac{a}{b}<0\]) thì \[a,b\]trái dấu.
+ Ta có: \[\frac{a}{b}>\frac{c}{d}\left( b,d>0 \right)\Leftrightarrow ad>bc\left( b,d>0 \right)\]
II. PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1. Sử dụng các kí hiệu
Sử dụng các kí hiệu \[\in ,\notin ,\subset ,\mathbb{N},\mathbb{Z},\mathbb{Q}\]
Cách giải:
Cần nắm vững ý nghĩa của từng kí hiệu:
– Kí hiệu \[\in \] đọc là “phần tử của” hoặc “thuộc”
– Kí hiệu \[\notin \] đọc là “không phải phần tử của” hoặc “không thuộc”
– Kí hiệu \[\subset \] đọc là “tập hợp con của”
– Kí hiệu \[\mathbb{N}\] chỉ tập hợp các số tự nhiên
– Kí hiệu \[\mathbb{Z}\] chỉ tập hợp các số nguyên
– Kí hiệu \[\mathbb{Q}\] chỉ tập hợp các số hữu tỉ
Dạng 2. Biểu diễn số hữu tỉ
Cách giải:
– Số hữu tỉ thường được biểu diễn dưới dạng phân số tối giản
– Khi biểu diễn số hữu tỉ trên trục số, ta thường viết số đó dưới dạng phân số tối giản có mẫu dương. Khi đó mẫu của phân số cho biết đoạn thẳng đơn vị cần được chia thành bao nhiêu phần bằng nhau.
Các bài toán thường gặp
Bài toán 1: Biểu diễn số hữu tỉ dưới dạng phân số rút gọn, và biểu diễn số hữu tỉ trên trục số
Bài toán 2: So sánh hai số hữu tỉ
III. GIẢI BÀI TẬP SÁCH GIÁO KHOA
Bài 1. (SGK Toán 7 tập 1 trang 7)
\[-3\in \mathbb{N}\]; \[-3\in \mathbb{Z}\]; \[-3\in \mathbb{Q}\]; \[\frac{-2}{3}\notin \mathbb{Z}\]; \[\frac{-2}{3}\in \mathbb{Q}\]; \[\mathbb{N}\subset \mathbb{Z}\subset \mathbb{Q}\]
Bài 2. (SGK Toán 7 tập 1 trang 7)
a) Ta có : \[\frac{3}{-4}=\frac{-3}{4}\]
Rút gọn các phân số đã cho ta được:
\[\frac{-12}{15}=\frac{-4}{3};\frac{-15}{20}=\frac{-5}{4};\frac{24}{-32}=\frac{-3}{4};\frac{-20}{28}=\frac{-5}{7};\frac{-27}{36}=\frac{-3}{4}\]
Vậy các phân số phải biểu diễn số hữu tỉ \[\frac{-3}{4}\]là: \[\frac{-3}{4}\],\[\frac{24}{-32}\],\[\frac{-27}{36}\]
b) Biểu diễn số hữu tỉ \[\frac{-3}{4}\]trên trục số:
Ta viết \[\frac{3}{-4}=\frac{-3}{4}\]và biểu diễn trên trục số như sau:
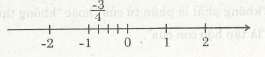
Bài 3. (SGK Toán 7 tập 1 trang 8)
a) Ta có: \[x=\frac{2}{-7}=\frac{-2}{7}=\frac{-22}{77};y=\frac{-3}{11}=\frac{-21}{77}\]
Ta thấy \[-22<-21\Rightarrow \frac{-22}{77}<\frac{-21}{77}\]. Vậy \[\frac{-2}{7}<\frac{-3}{11}\]hay \[x
b) Ta có: \[x=\frac{-213}{300};y=\frac{18}{-25}=\frac{-18}{25}=\frac{-216}{300}\]
Ta thấy \[-213>-216\Rightarrow \frac{-213}{300}>\frac{-216}{300}\]. Vậy \[x=\frac{-213}{300}>y=\frac{18}{-25}\].
c) \[x=-0,75=\frac{-75}{100}=\frac{-3}{4}\Rightarrow x=y\]
Bài 4. (SGK Toán 7 tập 1 trang 8)
Nhờ tính chất cơ bản của phân số, ta luôn có thể viết một phân số có mẫu âm thành một phân số bằng nó và có mẫu dương. Vì vậy, ta chỉ cần xét số hữu tỉ \[\frac{a}{b}\] \[\left( a,b\in \mathbb{Z},b\ne 0 \right)\]
Nếu \[a,b\]cùng dấu thì ta có \[\frac{a}{b}>0\]
Nếu \[a,b\]khác dấu thì ta có \[\frac{a}{b}<0\]
Bài 5. (SGK Toán 7 tập 1 trang 8)
Ta có \[x=\frac{a}{m},y=\frac{b}{m},z=\frac{a+b}{2m}\left( a,b\in \mathbb{Z},m>0 \right)\] và \[x
Ta chứng minh \[xhay \[\frac{a}{m}<\frac{a+b}{2m}\]. Ta có \[am
\[\Rightarrow \frac{a}{m}<\frac{a+b}{2m}\left( m>0 \right)\]. Vậy \[x
Lại có ta chứng minh \[zhay \[\frac{a+b}{2m}<\frac{b}{m}\]
Ta có \[am
\[\Rightarrow \frac{a+b}{2m}<\frac{b}{m}\left( m>0 \right)\]. Vậy \[z
Kết luận \[x (đpcm).
Trên đây là gợi ý giải bài tập Toán 7 Bài 1: Tập hợp Q các số hữu tỉ do giáo viên Ican trực tiếp biên soạn theo chương trình mới nhất. Chúc các bạn học tập vui vẻ
